Brief Intro to Binary Tree, Binary Search Tree, and Balanced BST

Bianry Tree

Binary tree is a tree data structure. Each node has at most two children, the left child and the right child.

// JavaScript
// Definition for a binary tree node
function TreeNode(key, left, right) {
    this.key = (key===undefined ? 0 : key)
    this.left = (left===undefined ? null : left)
    this.right = (right===undefined ? null : right)
}

Time complexity of operations (search, insertion, deletion) in binary tree is O(n),
since it has to traverse the whole tree.
How to reduce it?

Binary Search Tree (BST)

Binary Search Tree, as its name, is for binary search.
A valid BST is defined as follows:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

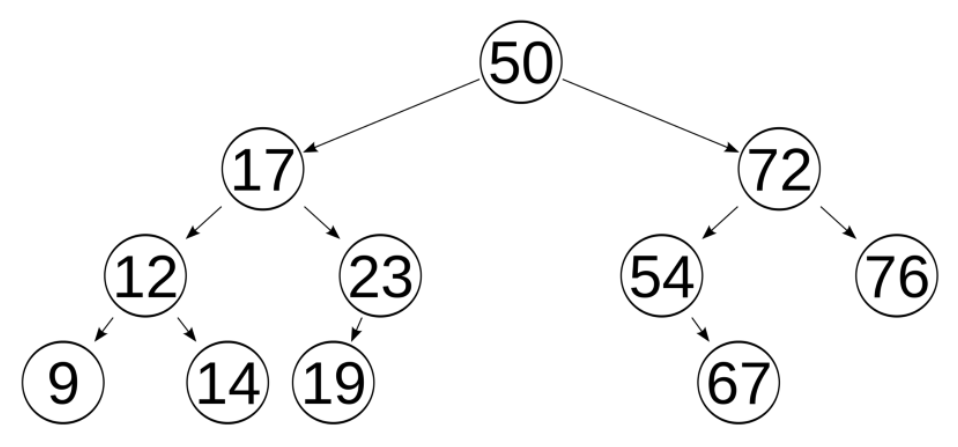
If target key is greater than current node key, search in right subtree, vice versa.
BST makes traversal into binary search, and time complexity of binary search is O(log n).
But if the tree is extremely unbalanced (all nodes in a chain), BST operations still be O(n).

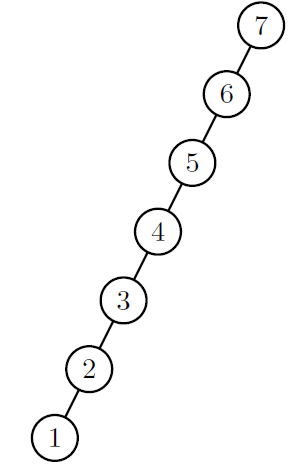
Balanced BST

Since height of the tree is the most important factor of time complexity, balancing the tree eliminates worst cases.
So time complexity is O(log n).